TensorFlow’s Adam optimizer. The Adam optimizer is a popular… | by Ikaro Silva | Jun, 2024

Some interesting notes the Adam [Kingma2014], that I found worth mentioning are:

• It is assumed that |m(t)/sqrt(v(t))| ~ 1 . In other words, the gradient average is larger than the variance. So that the change in θ(t) is bounded by α(t). I am not sure this is in general the case, and to what extent a typical hype-parameter optimization of α, β₁, and β₂ can make sure that this assumption is indeed guaranteed. If this assumption is not true, it is possible that we could observe exploding/vanishing gradients during training.
• The authors compare the term m(t)/sqrt(v(t)) to a Signal to Noise Ratio ( SNR ). In the sense that high SNR yields larger steps taken away from the gradient, and low SNR yields smaller steps away from the gradient ( a form of annealing ). This is in agreement, and to some extent re-assuring, with the analysis done in [Aitchison2018] where the authors unified SGD with Bayesian and Kalman filtering.
• Because of the assumption that SNR ~ 1 , there is an expectation that the neighborhood of the optimum α is known in advance. Alternatively, perhaps that explains why α should always be part of hyper-parameter tuning.
• v(t), the estimated variance, is a poor approximation for Convolutional Neural Networks ( in their experiment, vanishing to 0 ).
• The the use of additional constraints, such as L1/L2 regularizes, may affect these assumptions in ways that may render Adam sub-optimal. For example, under standard L2 regularization ( a.k.a., weight decay) it is known that Adam tends to under regularize the weights [Loshchilov2017].
• Because Adam does not use the Hessian matrix to compute higher derivatives, the gradient can be underestimated under negative curvature and overestimated under positive curvature. In particular, ill-conditioning of the gradient can occur when the second order term of the Taylor series expansion (including the Hessian term) is higher than v(t). When this happens, the gradient norm, |m(t)|, does not decrease significantly but but the second order term of the Taylor series expansion grows by orders of magnitude. Thus the learning is very slow because |m(t)/sqrt(v(t))|
• Adam is not guaranteed to converge or have a decreasing learning rate, specially in high dimensional setting where the v(t) can be large. In such cases, maintaining the maximum v(t) instead of performing weighted averaging may yield better results. In general any algorithm that relies on a fixed sized window to scale the gradient updates can fail to converge and have increased learning rates [Reddi2019].

As noted previously the forgetting factors ( β₁, β₂, and ema_momentum) control the window sizes in which the statistics are compute. Figure 1 below shows a plot of the time it takes for a unit sample to decay to 10% of its original value for different settings the forgetting factor. Note that values of β₁, β₂, and ema_momentum of less than 0.9 have an effective “memory”of less than 20 epochs, which can make the estimate of the statistics highly variable, but at the cost of being daptive to sudden changes.

More specifically, the impulse response of the weighted averaging filter is given by [Morrison1969]:

x[t] =βᵗ(1-β) for t≥1 (Equation 4)

And it’s Variance Reduction Factor (VRF) under standard unit Gaussian Noise is [Morrison1969]:

VRF(β)=(1-β)/(1+β) (Equation 5)

Finally, the following equation can be used to obtain the equivalent fixed filter length that yields the same VRF [Morrison1969]:

L = 2/ (1-β) ( Equations 6).

All the above analysis is summarized on Table 1 below for the default values of the β₁ and β₂ parameters in Adam. Note that β₂ default setting reduces the variance of white Gaussian noise (VRF) by 0.0005, or 105.2 times more than β₁, at a cost of a much larger “memory” or slower transient decay.

In this section we will create a simulation environment in TF that will allow us to test and explore with SGD with the Adam optimizer in a setting that is as close to a real application as possible, while allowing us to have objective knowledge the true loss function. The environment consists of 3 keys parts:

1. A customizable loss function that is defined in its entire domain
2. A very simple TF model with only one tunable parameter w, and whose performance at any value w is defined by the loss function in 1) above.
3. The training routine that performs initialization and the gradient descent on w .

The code for all these components and results can be found at:
https://github.com/ikarosilva/medium/blob/main/scripts/Adam.ipynb

Figure 2 shows the ideal loss function that we have implemented in TF. Figure 3 shows the derived m(t), v(t) and SNR from the custom loss in Figure 2. The values were derived based on Equation 3 and the first order point difference of the custom loss.

In order to make the simulation more realistic, and account for stochastic factors in both the input as well as in the loss curve estimation due to finite sample size, we also explore cases where the loss has a small amount of LogNormal noise (Figure 4).

Note that a key detail of the loss functions in Figure 2 and 4 is that the standard kernel initializers in TF ( GlorotNormal, GlorotUniform, HeNormal, and HeUniform) will tend to select initial conditions close to 0. Thus custom loss functions that a global minimum far from 0 and a peak between 0 and the global minimum may be difficult to optimize with these initializers. Nevertheless, this challenge may also be present in some loss functions we may encounter in real-world problems.

The simulation environment has a train_step() method that users a single output Dense layer only one parameter (passed as the output of the Keras model and accessible via self.trainable_variables ). The class is defined in the code snippet below.

class CustomModel(keras.Model):
def __init__(self,loss_func, *args, **kwargs):
super().__init__(*args, **kwargs)
self.loss_tracker = LastSample(name="loss")
self.w_metric = LastSample(name="weight")
self.momentum = LastSample(name="momentum")
self.velocity = LastSample(name="velocity")
self.loss_func=loss_func
def train_step(self, data):
trainable_vars = self.trainable_variables
self.w_metric.update_state(tf.squeeze(trainable_vars[0]))
with tf.GradientTape() as tape:
loss = self.loss_func(tf.squeeze(trainable_vars[0]))
gradients = tape.gradient(loss, trainable_vars)
self.optimizer.apply_gradients(zip(gradients, trainable_vars))
self.loss_tracker.update_state(tf.squeeze(loss))
#print(self.optimizer.variables()[1])
self.momentum.update_state(tf.squeeze(self.optimizer.variables()[1]))
self.velocity.update_state(tf.squeeze(self.optimizer.variables()[2]))
return {"loss": self.loss_tracker.result(), "weight": self.w_metric.result(), "momentum":self.momentum.result(), "velocity":self.velocity.result()}
@property
def metrics(self):
return [self.loss_tracker, self.w_metric, self.momentum, self.velocity]

The key part of this model is that we override the performance during training so that it is a direct function of the model’s single parameter w and our custom loss:

with tf.GradientTape() as tape:
loss = self.loss_func(tf.squeeze(trainable_vars[0]))

In this way the input training samples or data are not a function of the loss, and affects the training process only through the number of times the loss gets computed at each epoch.

The training component is the simplest part of the environment. In here we simply define a one parameter model ( with fixed initialization seed), and the dummy data to pass through TF’s training framework:

def run(optimizer,seed=0,loss_func=None):
initalizer=tf.keras.initializers.GlorotUniform(seed)
inputs = keras.Input(shape=(1,))
outputs = keras.layers.Dense(1,use_bias=False,kernel_initializer=initalizer)(inputs)
model = CustomModel(loss_func,inputs, outputs)
xtrain = np.random.random((1, 1))*0
ytrain = xtrain*TRUE_W
model.compile(optimizer=optimizer,run_eagerly=False)
history = model.fit(xtrain, ytrain, epochs=100,verbose=0,batch_size=128)
return history 

The training history is returned, which allow us to visualize and understand the behavior of the optimizer in the context of the true loss function defined above. Note that an optimizer is passed as input, this allows us to compare different optimizer settings with a consistent standard.

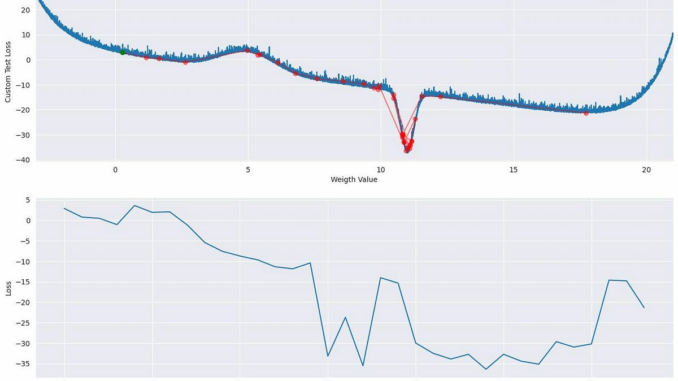
Figure 5 shows the results of the Adam optimizer on the clean custom loss function along with the respective learning curves across a sweep of β₁ and β₂ values. The algorithm fails to converge for for this sweep, in part because of the initialization close to 0, and the decreased gradient followed by a peak between 0 and the global minimum. Interesting a β₁=1 and/or β₂=1 are consistently worse than other values (no gradient change).

The hyper-paremeter optmization search on learning rate, β₁, β₂, ϵ, and intializer seed was done with Optuna (code snippet shown below).

def get_params(trial):
params = {"lr": trial.suggest_float("lr", 1e-3, 1),
"beta_1": trial.suggest_float("beta_1",0.5,0.99),
"beta_2": trial.suggest_categorical("beta_2",[0,0.1]),
"epsilon":trial.suggest_categorical("epsilon",[1e-8,1e-7,1e-6,1e-5]),
"seed":trial.suggest_categorical("seed",[0,1,2,3,4,5,6,7,8,9]),
}
return params
def get_objective():
def objective(trial):
params = get_params(trial)
optimizer=tf.keras.optimizers.Adam(learning_rate=params['lr'],beta_1=params['beta_1'],beta_2=params['beta_2'],epsilon=params['epsilon'])
history = run(optimizer=optimizer,seed=params['seed'],loss_func=custom_loss_tf)
score=history.history['loss'][-1]
score = 30 if np.isnan(score) else score
return score
return objective
def optuna_tuner(optuna_trials=100):
n_startup_trials=50
sampler = optuna.samplers.TPESampler(seed=10, n_startup_trials=n_startup_trials,consider_endpoints=True,multivariate=True)
study = optuna.create_study(sampler=sampler, direction="minimize")
objective = get_objective()
study.optimize(objective, n_trials=optuna_trials)
trial = study.best_trial
print("**"*50 + " Finished Optimizing")
print("Number of finished trials: ", len(study.trials))
print("  Value: {}".format(trial.value))
print("Best  Params: %s" % str(trial.params))
results=trial.params.copy()
return results
best_params = optuna_tuner(optuna_trials=100)

The results for this search resulted in the following best set of parameters:

Number of finished trials:  100
Value: -36.80474853515625
Best  Params: {'lr': 0.4637489790151759, 'beta_1': 0.8015293261694655, 'beta_2': 0, 'epsilon': 1e-08, 'seed': 3}

With SGD and learning curves shown in Figure 6 below. Interestingly, in this particular case choosing a value of β₂=0 yielded the best results. This perhaps suggests that for this loss, the gradient maybe changing too quickly for the default long averaging window given by 0.999.

Figure 7 shows the results of the Adam optimizer on the noisy custom loss function along with the respective learning curves across a sweep of β₁ and β₂ values. Similar to Figure 5, the algorithm fails to converge for for this sweep, in part because of the initialization close to 0, and the decreased gradient followed by a peak between 0 and the global minimum. Again, β₁=1 and/or β₂=1 are consistently worse than other values (no gradient change).

Similar to the clean loss case, the results for this search resulted in the following best set of parameters and learning curve (Figure 8):

umber of finished trials:  100
Value: -31.362701416015625
Best  Params: {'lr': 0.344019424394633, 'beta_1': 0.8077679923825423, 'beta_2': 0, 'epsilon': 1e-07, 'seed': 0}

Overall the results are very similar to the clean loss condition, although in the noisy case the best learning rate was smaller (0.344 vs 0.46) and ϵ was higher (1e-7 vs 1e-8).

For this final exploration we investigated if performance on the noisy loss could be further improved by using annealing via the cosine decay with restarts learning rate scheduler. The hypothesis here being, that the cosine decay with restarts could help overcome the limitations of the initialization values close to 0 and the peak between 0 and the global minimum in our loss function. We used the TF scheduler implemented in TF show in the code snippet below:

learning_rate=tf.keras.optimizers.schedules.CosineDecayRestarts(params['lr'],2)
optimizer=tf.keras.optimizers.Adam(learning_rate=learning_rate,beta_1=params['beta_1'],beta_2=params['beta_2'],epsilon=params['epsilon'])
h

The optuna search yielded the following best parameters:

Number of finished trials:  100
Value: -36.769046783447266
Best  Params: {'lr': 0.8871769570152, 'beta_1': 0.535195527321946, 'beta_2': 0, 'epsilon': 1e-05, 'seed': 4}

Figure 9 below shows the result of the SGD with the optimal settings for Adam and cosine decay with restarts.

Overall SGD with cosine decay with restarts yielded faster convergence ( also with a much higher learning rate), and with a more stable learning curve and better endpoint (final loss value of -36 compared to -31 without the annealing).

To summarize, in this article we:

1. Reviewed the algorithm behind Adam optimizer used for stochastic gradient descent
2. Quantified some of the characteristics of the exponential moving average filter that is used extensively in Adam to update it’s gradient statistics.
3. Created a environment in TF that allowed us to understand and judge Adam’s behavior using a known loss function, but as close as to a deployed environment as possible.
4. Discovered that, for the example loss function created, the default settings from Adam is far from optimal. However, use of Optuna to find the optimal hyper-parameters and annealing with cosine decay were crucial in the finding the global minimum and fast convergence of SGD.

Some future areas to explore on this analysis could be:

• Generating loss functions that are typical of real world problems by a deeper understanding or modeling of the geometry for certain applications.
• Mapping certain features of the training curve with the geometry of the loss function. In other words, what can we infer from the geometry of our loss function given the behavior of our training curve through the SGD process?
• For certain specific problems and neural network architectures (ie: Transformer and natural language processing) , collect all successfully trained neural network and their weights. Compile the weight distributions for all these trained models and see how they compare to the Glorot and He initialization distributions. Does a high Kullback–Leibler divergence between say the Glorot and final weights predict longer training timing ? Is there a bias on the final trained weights observed in the production models? Could the weights of production models follow power law behavior?
• In some cases can it be better to do short training bouts across wide range of intializer seeds versus a single long training session?
• Explore different variations of Adam such as AdamW, Adamax, and AMSGrad.

[Kingma2014] Kingma, Diederik P., and Jimmy Ba. “Adam: A method for stochastic optimization.” arXiv preprint arXiv:1412.6980 (2014).

[Aitchison2018] Aitchison, Laurence. “A unified theory of adaptive stochastic gradient descent as Bayesian filtering.” (2018).

[Loshchilov2017] Loshchilov, Ilya, and Frank Hutter. “Decoupled weight decay regularization.” arXiv preprint arXiv:1711.05101 (2017).

[Reddi2019] Reddi, Sashank J., Satyen Kale, and Sanjiv Kumar. “On the convergence of adam and beyond.” arXiv preprint arXiv:1904.09237 (2019).

[Goodfellow2016] Goodfellow, Ian, Yoshua Bengio, and Aaron Courville. Deep learning. MIT press, 2016.

[Morrison1969] Morrison, Norman. “Introduction to sequential smoothing and prediction.” (1969).