This is the final part of a two-part series about feature selection. Read part 1 here.
Brief recap: when fitting a model to a dataset, you may want to select a subset of the features (as opposed to using all features), for various reasons. But even if you have a clear objective function to search for the best combination of features, the search may take a long time if the number of features N is very large. Finding the best combination is not always easy. Brute-force searching generally does not work beyond several dozens of features. Heuristic algorithms are needed to perform a more efficient search.
If you have N features, what you’re looking for is an N-length vector [1, 1, 0, 0, 0, 1, ...] with values from {0, 1} . Each vector component corresponds to a feature. 0 means the feature is rejected, 1 means the feature is selected. You need to find the vector that minimizes the cost / objective function you’re using.
In the previous article, we’ve looked at a classic algorithm, SFS (sequential feature search), and compared it with an efficient evolutionary algorithm called CMA-ES. We’ve started with the House Prices dataset on Kaggle which, after some processing, yielded 213 features with 1453 observations each. The model we’ve tried to fit was statsmodels.api.OLS() and the objective function was the model’s BIC — Bayesian Information Criterion, a measure of information loss. Lower BIC means a better fit, so we’re trying to minimize the objective.
In this article, we will look at another evolutionary technique: genetic algorithms. The context (dataset, model, objective) remains the same.
Genetic algorithms are inspired by biological evolution and natural selection. In nature, living beings are (loosely speaking) selected for the genes (traits) that facilitate survival and reproductive success, in the context of the environment where they live.
Now think of feature selection. You have N features. You’re trying to find N-length binary vectors [1, 0, 0, 1, 1, 1, ...] that select the features (1 = feature selected, 0 = feature rejected) so as to minimize a cost / objective function.
Each such vector can be thought of as an “individual”. Each vector component (value 0 or value 1) becomes a “gene”. By applying evolution and selection, it might be possible to evolve a population of individuals in such a way as to get close to the best value for the objective function we’re interested in.
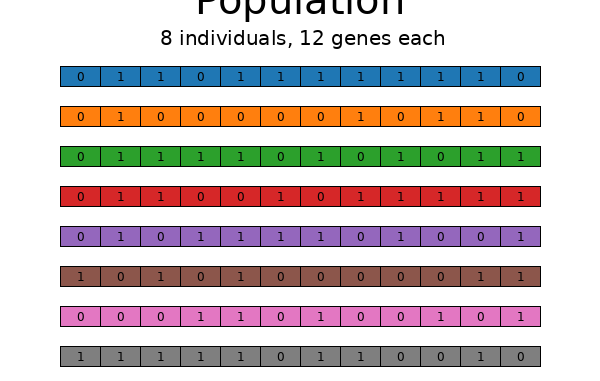
Here’s GA in a nutshell. Start by generating a population of individuals (vectors), each vector of length N. The vector component values (genes) are randomly chosen from {0, 1}. In the diagram below, N=12, and the population size is 8.
After the population is created, evaluate each individual via the objective function.
Now perform selection: keep the individuals with the best objective values, and discard those with the worst values. There are many possible strategies here, from naive ranking (which, counterintuitively, doesn’t work very well), to stochastic tournament selection, which is very efficient in the long run. Remember the explore-exploit dilemma. With GA, it’s very easy to fall into naive exploit traps that close the door to powerful exploration. GA is all about exploration. Here’s a short list of selection techniques, and check the links at the end for more info.
Once the best individuals have been selected, and the less fit ones have been discarded, it’s time to introduce variation in the gene pool via two techniques: crossover and mutation.
Crossover works exactly like in nature, when two living creatures are mating and producing offspring: genetic material from both parents is “mixed” in the descendants, with some degree of randomness.
Mutation, again, is pretty much what happens in nature when random mutations occur in the genetic material, and new values are introduced in the gene pool, increasing its diversity.
After all that, the algorithm loops back: the individuals are again evaluated via the objective function, selection occurs, then crossover, mutation, etc.
Various stopping criteria can be used: the loop may break if the objective function stops improving for some number of generations. Or you may set a hard stop for the total number of generations evaluated. Or do something time-based, or watch for an external signal, etc. Regardless, the individuals with the best objective values should be considered to be the “solutions” to the problem.
A few words about elitism: with stochastic selection techniques such as tournament, the best, absolute top individuals in a generation may actually not get selected, by pure chance — it’s unlikely, but it does happen. Elitism bypasses this, and simply decrees that the best must survive, no matter what. Elitism is an exploit technique. It may cause the algorithm to fall into local extremes, missing the global solution. Again, GA is all about exploration. My rather limited experience with GA seems to confirm the idea that an exploit bias is not beneficial for GA. But your mileage may vary; if you like to experiment with algorithm variants, GA gives you many opportunities to do so.
GA has several hyperparameters you can tune:
- population size (number of individuals)
- mutation probabilities (per individual, per gene)
- crossover probability
- selection strategies, etc.
Running trials by hand with various hyperparameter values is one way to figure out the best code. Or you could encapsulate GA in Optuna and let Optuna work on finding the best hyperparameters — but this is computationally expensive.
Here’s a simple GA code that can be used for feature selection. It uses the deap library, which is very powerful, but the learning curve may be steep. This simple version, however, should be clear enough.
# to maximize the objective
# fitness_weights = 1.0
# to minimize the objective
fitness_weights = -1.0# copy the original dataframes into local copies, once
X_ga = X.copy()
y_ga = y.copy()
# 'const' (the first column) is not an actual feature, do not include it
X_features = X_ga.columns.to_list()[1:]
try:
del creator.FitnessMax
del creator.Individual
except Exception as e:
pass
creator.create("FitnessMax", base.Fitness, weights=(fitness_weights,))
creator.create(
"Individual", array.array, typecode='b', fitness=creator.FitnessMax
)
try:
del toolbox
except Exception as e:
pass
toolbox = base.Toolbox()
# Attribute generator
toolbox.register("attr_bool", random.randint, 0, 1)
# Structure initializers
toolbox.register(
"individual",
tools.initRepeat,
creator.Individual,
toolbox.attr_bool,
len(X_features),
)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
def evalOneMax(individual):
# objective function
# create True/False selector list for features
# and add True at the start for 'const'
cols_select = [True] + [i == 1 for i in list(individual)]
# fit model using the features selected from the individual
lin_mod = sm.OLS(y_ga, X_ga.loc[:, cols_select], hasconst=True).fit()
return (lin_mod.bic,)
toolbox.register("evaluate", evalOneMax)
toolbox.register("mate", tools.cxTwoPoint)
toolbox.register("mutate", tools.mutFlipBit, indpb=0.05)
toolbox.register("select", tools.selTournament, tournsize=3)
random.seed(0)
pop = toolbox.population(n=300)
hof = tools.HallOfFame(1)
pop, log = algorithms.eaSimple(
pop, toolbox, cxpb=0.5, mutpb=0.2, ngen=10, halloffame=hof, verbose=True
)
best_individual_ga_small = list(hof[0])
best_features_ga_small = [
X_features[i] for i, val in enumerate(best_individual_ga_small) if val == 1
]
best_objective_ga_small = (
sm.OLS(y_ga, X_ga[['const'] + best_features_ga_small], hasconst=True)
.fit()
.bic
)
print(f'best objective: {best_objective_ga_small}')
print(f'best features: {best_features_ga_small}')
The code creates the objects that define an individual and the whole population, along with the strategies used for evaluation (objective function), crossover / mating, mutation, and selection. It starts with a population of 300 individuals, and then calls eaSimple() (a canned sequence of crossover, mutation, selection) which runs for only 10 generations, for simplicity. Hall of fame with a size of 1 is defined, where the absolute best individual is preserved against being accidentally mutated / skipped during selection, etc.
Hall of fame is not elitism. Hall of fame copies the best individual from the population, and only keeps the copy in a tin can. Elitism preserves the best individual in the population from one generation to the next.
This simple code is easy to understand, but inefficient. Check the notebook in the repository for a more complex version of the GA code, which I am not going to quote here. However, running the more complex, optimized code from the notebook for 1000 generations produces these results:
best objective: 33705.569572544795
best generation: 787
objective runs: 600525
time to best: 157.604 sec
And here’s the entire history of the full, optimized GA code from the notebook, running for 1000 generations, trying to find the best features. From left to right, the heatmap indicates the popularity of each feature within the population across generations (brighter shade = more popular). You can see how some features are always popular, others are rejected quickly, while yet others may become more popular or less popular as time goes by.

Be the first to comment