Mastering Customer Segmentation with LLMs

This is the most common method and the one you will surely know. Anyway, we are going to study it because I will show advanced analysis techniques in these cases. The Jupyter notebook where you will find the complete procedure is called kmeans.ipynb

Preprocessed

A preprocessing of the variables is carried out:

1. It consists of converting categorical variables into numeric ones. We can apply a Onehot Encoder (the usual thing) but in this case we will apply an Ordinal Encoder.
2. We try to ensure that the numerical variables have a Gaussian distribution. For them we will apply a PowerTransformer.

Let’s see how it looks in code.

import pandas as pd # dataframe manipulation
import numpy as np # linear algebra
# data visualization
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import plotly.express as px
import plotly.graph_objects as go
import seaborn as sns
import shap
# sklearn 
from sklearn.cluster import KMeans
from sklearn.preprocessing import PowerTransformer, OrdinalEncoder
from sklearn.pipeline import Pipeline
from sklearn.manifold import TSNE
from sklearn.metrics import silhouette_score, silhouette_samples, accuracy_score, classification_report
from pyod.models.ecod import ECOD
from yellowbrick.cluster import KElbowVisualizer
import lightgbm as lgb
import prince
df = pd.read_csv("train.csv", sep = ";")
df = df.iloc[:, 0:8]
pipe = Pipeline([('ordinal', OrdinalEncoder()), ('scaler', PowerTransformer())])
pipe_fit = pipe.fit(df)
data = pd.DataFrame(pipe_fit.transform(df), columns = df.columns)
data

Output:

Outliers

It is crucial that there are as few outliers in our data as Kmeans is very sensitive to this. We can apply the typical method of choosing outliers using the z score, but in this post I will show you a much more advanced and cool method.

Well, what is this method? Well, we will use the Python Outlier Detection (PyOD) library. This library is focused on detecting outliers for different cases. To be more specific we will use the ECOD method (“empirical cumulative distribution functions for outlier detection”).

This method seeks to obtain the distribution of the data and thus know which are the values ​​where the probability density is lower (outliers). Take a look at the Github if you want.

from pyod.models.ecod import ECOD
clf = ECOD()
clf.fit(data)
outliers = clf.predict(data) 
data["outliers"] = outliers
# Data without outliers
data_no_outliers = data[data["outliers"] == 0]
data_no_outliers = data_no_outliers.drop(["outliers"], axis = 1)
# Data with Outliers
data_with_outliers = data.copy()
data_with_outliers = data_with_outliers.drop(["outliers"], axis = 1)
print(data_no_outliers.shape) -> (40691, 8)
print(data_with_outliers.shape) -> (45211, 8)

Modeling

One of the disadvantages of using the Kmeans algorithm is that you must choose the number of clusters you want to use. In this case, in order to obtain that data, we will use Elbow Method. It consists of calculating the distortion that exists between the points of a cluster and its centroid. The objective is clear, to obtain the least possible distortion. In this case we use the following code:

from yellowbrick.cluster import KElbowVisualizer
# Instantiate the clustering model and visualizer
km = KMeans(init="k-means++", random_state=0, n_init="auto")
visualizer = KElbowVisualizer(km, k=(2,10))
visualizer.fit(data_no_outliers)        # Fit the data to the visualizer
visualizer.show()    

Output:

We see that from k=5, the distortion does not vary drastically. It is true that the ideal is that the behavior starting from k= 5 would be almost flat. This rarely happens and other methods can be applied to be sure of the most optimal number of clusters. To be sure, we could perform a Silhoutte visualization. The code is the following:

from sklearn.metrics import davies_bouldin_score, silhouette_score, silhouette_samples
import matplotlib.cm as cm
def make_Silhouette_plot(X, n_clusters):
plt.xlim([-0.1, 1])
plt.ylim([0, len(X) + (n_clusters + 1) * 10])
clusterer = KMeans(n_clusters=n_clusters, max_iter = 1000, n_init = 10, init = 'k-means++', random_state=10)
cluster_labels = clusterer.fit_predict(X)
silhouette_avg = silhouette_score(X, cluster_labels)
print(
"For n_clusters =", n_clusters,
"The average silhouette_score is :", silhouette_avg,
)
# Compute the silhouette scores for each sample
sample_silhouette_values = silhouette_samples(X, cluster_labels)
y_lower = 10
for i in range(n_clusters):
ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_clusters)
plt.fill_betweenx(
np.arange(y_lower, y_upper),
0,
ith_cluster_silhouette_values,
facecolor=color,
edgecolor=color,
alpha=0.7,
)
plt.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 10
plt.title(f"The Silhouette Plot for n_cluster = {n_clusters}", fontsize=26)
plt.xlabel("The silhouette coefficient values", fontsize=24)
plt.ylabel("Cluster label", fontsize=24)
plt.axvline(x=silhouette_avg, color="red", linestyle="--")
plt.yticks([])  
plt.xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
range_n_clusters = list(range(2,10))
for n_clusters in range_n_clusters:
print(f"N cluster: {n_clusters}")
make_Silhouette_plot(data_no_outliers, n_clusters)   
plt.savefig('Silhouette_plot_{}.png'.format(n_clusters))
plt.close()
OUTPUT:
"""
N cluster: 2
For n_clusters = 2 The average silhouette_score is : 0.1775761520337095
N cluster: 3
For n_clusters = 3 The average silhouette_score is : 0.20772622268785523
N cluster: 4
For n_clusters = 4 The average silhouette_score is : 0.2038116470937145
N cluster: 5
For n_clusters = 5 The average silhouette_score is : 0.20142888327171368
N cluster: 6
For n_clusters = 6 The average silhouette_score is : 0.20252892716996912
N cluster: 7
For n_clusters = 7 The average silhouette_score is : 0.21185490763840265
N cluster: 8
For n_clusters = 8 The average silhouette_score is : 0.20867816457291538
N cluster: 9
For n_clusters = 9 The average silhouette_score is : 0.21154289421300868
"""

It can be seen that the highest silhouette score is obtained with n_cluster=9, but it is also true that the variation in the score is quite small if we compare it with the other scores. At the moment the previous result does not provide us with much information. On the other hand, the previous code creates the Silhouette visualization, which gives us more information:

Since understanding these representations well is not the goal of this post, I will conclude that there seems to be no very clear decision as to which number is best. After viewing the previous representations, we can choose K=5 or K= 6. This is because for the different clusters, their Silhouette score is above the average value and there is no imbalance in cluster size. Furthermore, in some situations, the marketing department may be interested in having the smallest number of clusters/types of customers (This may or may not be the case).

Finally we can create our Kmeans model with K=5.

km = KMeans(n_clusters=5,
init='k-means++', 
n_init=10,
max_iter=100, 
random_state=42)
clusters_predict = km.fit_predict(data_no_outliers)
"""
clusters_predict -> array([4, 2, 0, ..., 3, 4, 3])
np.unique(clusters_predict) -> array([0, 1, 2, 3, 4])
"""

Evaluation

The way of evaluating kmeans models is somewhat more open than for other models. We can use

• metrics
• visualizations
• interpretation (Something very important for companies).

In relation to the model evaluation metrics, we can use the following code:

from sklearn.metrics import silhouette_score
from sklearn.metrics import calinski_harabasz_score
from sklearn.metrics import davies_bouldin_score
"""
The Davies Bouldin index is defined as the average similarity measure 
of each cluster with its most similar cluster, where similarity 
is the ratio of within-cluster distances to between-cluster distances.
The minimum value of the DB Index is 0, whereas a smaller 
value (closer to 0) represents a better model that produces better clusters.
"""
print(f"Davies bouldin score: {davies_bouldin_score(data_no_outliers,clusters_predict)}")
"""
Calinski Harabaz Index -> Variance Ratio Criterion.
Calinski Harabaz Index is defined as the ratio of the 
sum of between-cluster dispersion and of within-cluster dispersion.
The higher the index the more separable the clusters.
"""
print(f"Calinski Score: {calinski_harabasz_score(data_no_outliers,clusters_predict)}")
"""
The silhouette score is a metric used to calculate the goodness of 
fit of a clustering algorithm, but can also be used as 
a method for determining an optimal value of k (see here for more).
Its value ranges from -1 to 1.
A value of 0 indicates clusters are overlapping and either
the data or the value of k is incorrect.
1 is the ideal value and indicates that clusters are very 
dense and nicely separated.
"""
print(f"Silhouette Score: {silhouette_score(data_no_outliers,clusters_predict)}")
OUTPUT:
"""
Davies bouldin score: 1.5480952939773156
Calinski Score: 7646.959165727562
Silhouette Score: 0.2013600389183821
"""

As far as can be shown, we do not have an excessively good model. Davies’ score is telling us that the distance between clusters is quite small.

This may be due to several factors, but keep in mind that the energy of a model is the data; if the data does not have sufficient predictive power, you cannot expect to achieve exceptional results.

For visualizations, we can use the method to reduce dimensionality, PCA. For them we are going to use the Prince library, focused on exploratory analysis and dimensionality reduction. If you prefer, you can use Sklearn’s PCA, they are identical.

First we will calculate the principal components in 3D, and then we will make the representation. These are the two functions performed by the previous steps:

import prince
import plotly.express as px
def get_pca_2d(df, predict):
pca_2d_object = prince.PCA(
n_components=2,
n_iter=3,
rescale_with_mean=True,
rescale_with_std=True,
copy=True,
check_input=True,
engine='sklearn',
random_state=42
)
pca_2d_object.fit(df)
df_pca_2d = pca_2d_object.transform(df)
df_pca_2d.columns = ["comp1", "comp2"]
df_pca_2d["cluster"] = predict
return pca_2d_object, df_pca_2d
def get_pca_3d(df, predict):
pca_3d_object = prince.PCA(
n_components=3,
n_iter=3,
rescale_with_mean=True,
rescale_with_std=True,
copy=True,
check_input=True,
engine='sklearn',
random_state=42
)
pca_3d_object.fit(df)
df_pca_3d = pca_3d_object.transform(df)
df_pca_3d.columns = ["comp1", "comp2", "comp3"]
df_pca_3d["cluster"] = predict
return pca_3d_object, df_pca_3d
def plot_pca_3d(df, title = "PCA Space", opacity=0.8, width_line = 0.1):
df = df.astype({"cluster": "object"})
df = df.sort_values("cluster")
fig = px.scatter_3d(
df, 
x='comp1', 
y='comp2', 
z='comp3',
color='cluster',
template="plotly",
# symbol = "cluster",
color_discrete_sequence=px.colors.qualitative.Vivid,
title=title).update_traces(
# mode = 'markers',
marker={
"size": 4,
"opacity": opacity,
# "symbol" : "diamond",
"line": {
"width": width_line,
"color": "black",
}
}
).update_layout(
width = 800, 
height = 800, 
autosize = True, 
showlegend = True,
legend=dict(title_font_family="Times New Roman",
font=dict(size= 20)),
scene = dict(xaxis=dict(title = 'comp1', titlefont_color = 'black'),
yaxis=dict(title = 'comp2', titlefont_color = 'black'),
zaxis=dict(title = 'comp3', titlefont_color = 'black')),
font = dict(family = "Gilroy", color  = 'black', size = 15))
fig.show()

Don’t worry too much about those functions, use them as follows:

pca_3d_object, df_pca_3d = pca_plot_3d(data_no_outliers, clusters_predict)
plot_pca_3d(df_pca_3d, title = "PCA Space", opacity=1, width_line = 0.1)
print("The variability is :", pca_3d_object.eigenvalues_summary)

Output:

It can be seen that the clusters have almost no separation between them and there is no clear division. This is in accordance with the information provided by the metrics.

Something to keep in mind and that very few people keep in mind is the PCA and the variability of the eigenvectors.

Let’s say that each field contains a certain amount of information, and this adds its bit of information. If the accumulated sum of the 3 main components adds up to around 80% variability, we can say that it is acceptable, obtaining good results in the representations. If the value is lower, we have to take the visualizations with a grain of salt since we are missing a lot of information that is contained in other eigenvectors.

The next question is obvious: What is the variability of the PCA executed?

The answer is the following:

As can be seen, we have 48.37% variability with the first 3 components, something insufficient to draw informed conclusions.

It turns out that when a PCA analysis is run, the spatial structure is not preserved. Luckily there is a less known method, called t-SNE, that allows us to reduce the dimensionality and also maintains the spatial structure. This can help us visualize, since with the previous method we have not had much success.

If you try it on your computers, keep in mind that it has a higher computational cost. For this reason, I sampled my original dataset and it still took me about 5 minutes to get the result. The code is as follows:

from sklearn.manifold import TSNE
sampling_data = data_no_outliers.sample(frac=0.5, replace=True, random_state=1)
sampling_clusters = pd.DataFrame(clusters_predict).sample(frac=0.5, replace=True, random_state=1)[0].values
df_tsne_3d = TSNE(
n_components=3, 
learning_rate=500, 
init='random', 
perplexity=200, 
n_iter = 5000).fit_transform(sampling_data)
df_tsne_3d = pd.DataFrame(df_tsne_3d, columns=["comp1", "comp2",'comp3'])
df_tsne_3d["cluster"] = sampling_clusters
plot_pca_3d(df_tsne_3d, title = "PCA Space", opacity=1, width_line = 0.1)

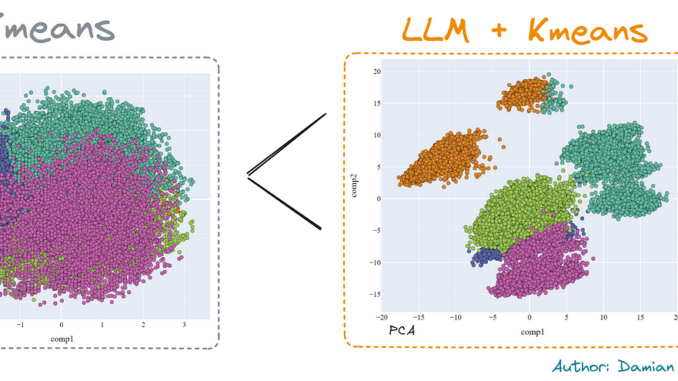
As a result, I got the following image. It shows a greater separation between clusters and allows us to draw conclusions in a clearer way.

In fact, we can compare the reduction carried out by the PCA and by the t-SNE, in 2 dimensions. The improvement is clear using the second method.

Finally, let’s explore a little how the model works, in which features are the most important and what are the main characteristics of the clusters.

To see the importance of each of the variables we will use a typical “trick” in this type of situation. We are going to create a classification model where the “X” is the inputs of the Kmeans model, and the “y” is the clusters predicted by the Kmeans model.

The chosen model is an LGBMClassifier. This model is quite powerful and works well having categorical and numerical variables. Having the new model trained, using the SHAP library, we can obtain the importance of each of the features in the prediction. The code is:

import lightgbm as lgb
import shap
# We create the LGBMClassifier model and train it
clf_km = lgb.LGBMClassifier(colsample_by_tree=0.8)
clf_km.fit(X=data_no_outliers, y=clusters_predict)
#SHAP values
explainer_km = shap.TreeExplainer(clf_km)
shap_values_km = explainer_km.shap_values(data_no_outliers)
shap.summary_plot(shap_values_km, data_no_outliers, plot_type="bar", plot_size=(15, 10))

Output:

It can be seen that feature housing has the greatest predictive power. It can also be seen that cluster number 4 (green) is mainly differentiated by the loan variable.

Finally we must analyze the characteristics of the clusters. This part of the study is what is decisive for the business. For them we are going to obtain the means (for the numerical variables) and the most frequent value (categorical variables) of each of the features of the dataset for each of the clusters:

df_no_outliers = df[df.outliers == 0]
df_no_outliers["cluster"] = clusters_predict
df_no_outliers.groupby('cluster').agg(
{
'job': lambda x: x.value_counts().index[0],
'marital': lambda x: x.value_counts().index[0],
'education': lambda x: x.value_counts().index[0],
'housing': lambda x: x.value_counts().index[0],
'loan': lambda x: x.value_counts().index[0],
'contact': lambda x: x.value_counts().index[0],
'age':'mean',
'balance': 'mean',
'default': lambda x: x.value_counts().index[0],
}
).reset_index()

Output:

We see that the clusters with job=blue-collar do not have a great differentiation between their characteristics. This is something that is not desirable since it is difficult to differentiate the clients of each of the clusters. In the job=management case, we obtain better differentiation.

After carrying out the analysis in different ways, they converge on the same conclusion: “We need to improve the results”.