After countless hours of trying things with the length of the training data, batch size, epoch size, etc., I’ve decided to step back, try to simplify the whole thing, and have a look at the internals of the model.
Simplified encoder / decoder
During the testing, it was very confusing, that all the token-indexes and the characters themselves have a detached meaning, which was only obtainable when I read through the whole file. I went with the direct ASCII 7bit implementation, and cut at character 122 (small cap z). Zero could be used for masking, as it represents “null”, and I won’t expect it in files.
Yes, there would be blind spots in the embedding, but at this stage, it’s interesting enough to see what the model does with weights that are not learning.
Reverting back to 1-length inputs
Andrej himself stated, that in that form, we are essentially implemented a bigram model, which only uses the last character for generation, so I could optimize for that.
Re-inspecting the modell
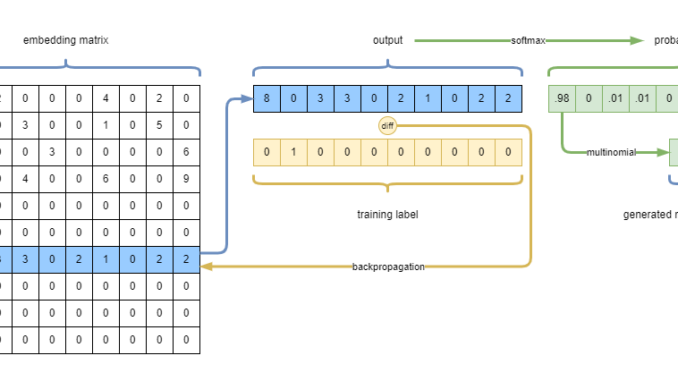
Sometimes it’s just good to visualize what is happening inside the model. I drew a sketch about what this model does:
What we are really doing, is getting the x-th row indicated by the input, from the embedding matrix, then softmax-ing and choosing the index of the character, that fits the probability curve encoded in the row of the embedding (multinomial).
During the learning, the loss (categorical cross-entropy) and gradient calculation / backpropagation will force the the embedding matrix’s relevant row to be closer to the training label. Essentially, the embedding matrix’s rows will represent the probabilities of the following characters. In our test, this will be a 123×123 matrix, as each character can be followed by any character.
Tool for inspecting the modell weight
I like to preserve things and found it handy to have a utility function, that can write the embedding matrix to the hard drive, where Excel can process it.
function saveEmbeddingValues(m: tf.LayersModel, fileName: string) {
console.log("The whole matrix as-is, and saved to this file:", fileName);
try { fs.unlinkSync(fileName); } catch (e) {
console.warn(`can't delete file [${fileName}]`)
}
(<number[][]>m.getLayer("embedding").getWeights()[0].arraySync()).forEach(item => {
fs.appendFile(fileName, `${item.toString()}\n`, err => {
if (err) throw err;
});
});
}
Yes, good old Excel does the trick with conditional formatting and dragable chart-data.
Expectations
If we assume, that the embedding matrix should resemble a probability matrix, we can directly calculate it, since we have access to all the data. It’s really simple, just set up a 2D array with zeros, cycle through the whole file, and increase the counter at x,y position where x is the current character, an y is the next character’s id.
Please note, this method only works because we have a direct relation of the embedding matrix’s values to the output probabilities.
Eventually, you’ll get something like this:
The good stuff happens in the lower right corner, where small caps alphanumeric characters reside. Above them are the large caps. The left and top lines are punctuation marks, space and enter characters. All the greens are non-existing transitions.
As we have all the numbers, we can do a proper probability calculation by dividing every element with the sum of it’s row. This is our final expectation for a transition probability:
To make comparisons easier, let’s chart the last letter separately:
Examining fitted weights
Let’s compare our expectation what we’ve got after the fitting, using ADAM as optimizer, for 1 epoch, with the batch of 32, and training on the whole 1.115.393 data points. The whole process takes less than 5 minutes tfjs-node, and we get the following result for the embedding matrix:
So the softmax-ed result is pretty much uniform, even tough we have some increases in original values at the right places. So this is the reason we generate gibberish: there are no significant differences in the values of the distribution.
Initial model weights
When you create an embedding layer (as shown above), the weights are initialized with a random uniform distribution (check it in the source: https://github.com/tensorflow/tfjs/blob/tfjs-v4.15.0/tfjs-layers/src/layers/embeddings.ts, line 88). One row will look like this:
When this tensor is used as-is for generation, it will produce giberris — no wonder, whe haven’t trained it at all. The yellow lines show the softmax-ed distribution, the generator will use, and it’s pretty much uniform, meaning this will produce random output.
My intuition is that we don’t need negative numbers, as we try to represent probabilities, and it seems like a good idea to give the model a meaningful starting point, where it can ascend/descend from/to during the training:
const logitsLayer = tf.layers.embedding({
embeddingsInitializer: tf.initializers.constant({value: 1.0/123.0})
});
The initializer can be set with a string, or an object:
- “zeros”: all the weights will be zeros. The problem with this, is if everyhting is zero, during the calculation, the model will encounter a division-by-zero problem, so at the end you’ll only get NaN as weights. Don’t us this
- “ones”: all the weights will be ones. This is quite convenient, as you can spot the ones in the weight matrix easily during investigation. You know, if you spot 1 anywhere, it wasn’t touched by the backpropagation.
- constant: as in the example. I’ve just specified uniform distribution that adds up to one. This is meaningful, so I’ve stuck with that.
Regulating weights with constraints
One idea was, that we shouldn’t allow the model to take on negative weight values, as probabilities are zero or positive. So let’s try it. One would add an embeddingConstraint parameter to the layer’s arguments, like this:
const logitsLayer = tf.layers.embedding({
embeddingsConstraint: tf.constraints.nonNeg()
});
What this does, is each time the embedding matrix (which is stored in a LayerVariable) is updated, it will go through a ReLU activation, which sets negative values to zero, and leaves the positive ones intact. (Check details here: https://github.com/tensorflow/tfjs/blob/tfjs-v4.15.0/tfjs-layers/src/variables.ts, line 103)
After training we get something like this:
Let’s examine the results:
- The softmax-ed values now resemble something I’d expect fom a probability distribution, so that’s a win
- Even though the layer has the noNeg() constraint set, there are lot’s of values that are negative. I need to debug even more in depth.
- Examining the embedding vectors for other letters showed the same pattern: softmax-ed results are okay-ish, but negative values where everywhere in the original weight matrix.
Let’s consider this a half win.
Generating stochastic responses with multinomial()
In the simplified model, which focuses only on one character, there’s no need for slice-and-dicing:
function generate(model: tf.LayersModel, idx: tf.Tensor, maxTokens: number) {
let ret = idx;
for (let i = 0; i < maxTokens; i++) {
const logits = <tf.Tensor>model.predictOnBatch(ret);
const probs = <tf.Tensor2D>logits.squeeze([1]).softmax();
// const predictedValue = probs.topk(1).indices.squeeze([1, 1]);
const predictedValue = tf.multinomial(probs, 1, undefined, true)
ret = ret.concat(predictedValue.cast('float32').expandDims(1));
}
console.log("Generated result:", decode(<number[]>ret.arraySync()));
}
I’ve noticed, that using this method, the generated text would often go in an endless loop. This is an indication that one letter refers to a letter that refers back to the first letter, making the thing cyclic.
I wasn’t familiar with the multinomial() function, so here’s the gist of it: you give it a tensor with probabilities of each bin, and tell the function to draw x number of values. Multinomial will present you a tensor, that contains the bin numbers in a return tensor, that has the same distribution as the original data you provided. Apparently, is used in NLP applications to evade the kinds of loops, I’ve ran into.
I had a hunch, that using multinomial(probs, 1) (so, you just draw one from the sample), will always result in drawing the bin with the largest probability, essentially making the result equal to topk(probs, 1), which select the highest number in a tensor.
Let’s test this, and generate 20 instances (draws) 20 times (sessions), and examine the resulting distributions on a simple [.66, .24, .10] probabilities for bins indicated by 0, 1, 2:
So, some interesting observations:
- the first draw is always the largest probability, essentially making it a constant. So don’t use multinomial(1), use topk(1) instead, otherwise you delude yourself by thinking doing the right thing.
- multinomial() is VERY probabilistic. If you check the resulting histograms, you’ll see that only in 3 cases out of 20 sessions have something close to the original, intended distribution
- there are cases where the distributions are plainly wrong, generating higher representation for values that are marked to have lower probabilities
My advice: use multinomial(2), and only use the second draw as a result, ditch / slice out the first (static) result

Be the first to comment