
In the intricate realm of supply chain management, the timely delivery of goods is a critical success factor. Evaluating supplier performance requires data-driven insights, and Minitab, the leading statistical software, provides a powerful yet easy-to-use solution. This blog will guide you through using Minitab’s 2-Proportion Test to analyze the rate of late deliveries between two suppliers – Supplier A and Supplier B. By delving into the data and performing the 2-Proportion Test, we aim to discern which supplier exhibits a higher rate of late deliveries.
WHAT IS A 2-PROPORTION TEST?
Minitab’s 2-Proportion Test, an essential tool in the field of statistics, enables us to compare the proportions of two groups and ascertain whether they are significantly different. In our context, the groups represent the rates of late deliveries for Supplier A and Supplier B.
LAYING THE FOUNDATION: THE HYPOTHESES
Before conducting the analysis, let’s define our hypotheses:
- Null Hypothesis (H0): There is no significant difference in the rates of late deliveries between Supplier A and Supplier B.
- Alternative Hypothesis (Ha): There is a significant difference in the rates of late deliveries between Supplier A and Supplier B.
UNVEILING THE DATA
Our analysis is based on the following data:
- Supplier A: Total deliveries = 1160, Late deliveries = 140
- Supplier B: Total deliveries = 1169, Late deliveries = 115
Based on these data points – without Minitab’s help – we might assume the alternative hypothesis is correct. In fact, we may even go as far as saying that supplier A is late 12% of the time and Supplier B is late 9.8% of the time.
Before we make a business decision that could impact our relationships with suppliers or customers, let’s put our data to the test.
EXECUTING THE 2-PROPORTION TEST IN MINITAB
Step 1: Open Minitab and navigate to “Stat” > “Basic Statistics” > “2 Proportions…” to launch the 2-Proportion Test dialog box.
Step 2: Enter the data into the dialog box:
- “Number of events” for Supplier A (late deliveries) = 140
- “Number of trials” for Supplier A (total deliveries) = 1160
- Repeat the same for Supplier B
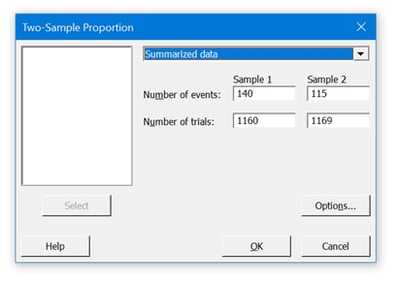
Step 3: Select your significance level and specify your alternative hypothesis. The most common (and acceptable) confidence level is 95% – which means you have only a 5% chance of being wrong.
Step 4: Click “OK” to generate the results.
INTERPRETING THE OUTCOMES
Minitab provides us with crucial insights including the test statistic, p-value, and confidence interval. Our focus rests on the p-value – a pivotal indicator that measures the likelihood of obtaining results as extreme as observed, assuming the null hypothesis is valid.
DRAWING THE VERDICT
Comparing the p-value with our chosen significance level (0.05), we draw conclusions as follows:
- If p-value < 0.05: Reject the null hypothesis. A significant difference in late delivery rates exists.
- If p-value ≥ 0.05: Fail to reject the null hypothesis. No significant difference in late delivery rates is evident.
CONCLUSION
Upon performing the 2-Proportion Test in Minitab, we discover that the p-value exceeds 0.05. This leads us to “Fail to reject the null hypothesis.” In simpler terms, no statistical evidence emerges to support the claim that Supplier A’s late delivery rate differs significantly from Supplier B’s. Therefore, concluding that one of these suppliers has a higher rate of late deliveries could be a mistake.
EMPOWERING INFORMED CHOICES
By harnessing Minitab’s 2-Proportion Test, we’ve unlocked an impartial assessment of supplier performance. Such evidence-based insights guide us in making informed decisions regarding supplier selection and management. Navigating the complex waters of supply chain management is facilitated by Minitab’s analytical prowess, propelling us toward data-driven efficiency and excellence.
See how Minitab can transform your supply chain data with a 30-day free trial


Be the first to comment