Introduction
In the realm of mathematics, physics, computer science, and beyond, tensors have emerged as versatile and indispensable constructs that underpin various aspects of contemporary scientific research and technological advancements. Tensors, often referred to as the mathematical extension of scalars, vectors, and matrices, provide a powerful framework for representing and manipulating multidimensional data. This essay delves into the world of tensors, exploring their origins, mathematical properties, and diverse applications across various domains.
The Multidimensional Constructs of Modern Science, weaving the fabric of understanding across the vast tapestry of knowledge.
I. The Genesis of Tensors
The concept of tensors can be traced back to the 19th century, primarily attributed to the mathematical genius of August Ferdinand Möbius and independently developed by Bernhard Riemann. However, it was the pioneering work of Gregorio Ricci-Curbastro and Tullio Levi-Civita in the late 19th and early 20th centuries that formalized the modern tensor calculus. Their efforts laid the foundation for tensors’ systematic study, as well as their integration into the fabric of physics, particularly in Albert Einstein’s theory of General Relativity.
II. Mathematical Underpinnings of Tensors
A tensor is a multidimensional array of numbers or other mathematical objects that follow certain transformation rules. In a formal sense, tensors can be defined through their transformation properties, which distinguish them from scalars, vectors, and matrices. Tensors exhibit rank, which denotes the number of indices required to specify a component, and covariant and contravariant transformations, which ensure consistency across different coordinate systems.
1. Rank of Tensors:
— Scalars: Rank-0 tensors, representing single values with no indices.
— Vectors: Rank-1 tensors, possessing one contravariant index.
— Matrices: Rank-2 tensors, featuring two indices (one covariant and one contravariant).
— Higher-order Tensors: Rank-n tensors, where n denotes the number of indices, can represent multidimensional data.
2. Covariant and Contravariant Transformation: Tensors can transform between covariant and contravariant forms based on the choice of coordinate systems. This transformation preserves the intrinsic properties of the tensor while adapting to different reference frames.
III. Applications of Tensors
The versatility of tensors extends across numerous scientific and technological disciplines:
1. Physics:
— General Relativity: Tensors play a pivotal role in describing the curvature of spacetime, enabling the formulation of Einstein’s field equations.
— Electromagnetism: Maxwell’s equations are elegantly expressed in tensor notation.
— Quantum Mechanics: Quantum states and operators can be represented as tensors, facilitating quantum computations.
2. Engineering:
— Structural Mechanics: Tensors are used to analyze stress and strain in materials, aiding in the design of safe and efficient structures.
— Fluid Dynamics: Tensor calculus is vital for understanding the behavior of fluids in engineering applications.
3. Computer Science and Machine Learning:
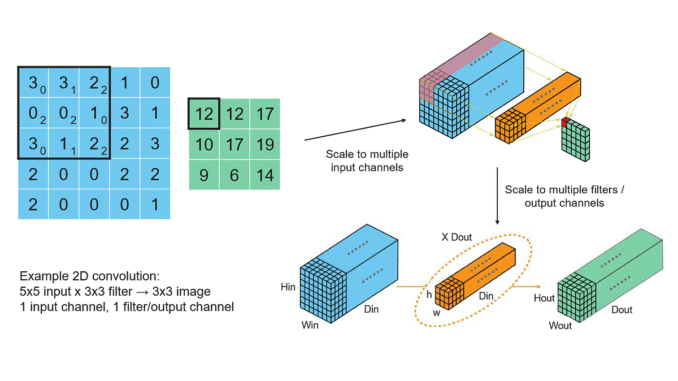
— Deep Learning: Convolutional neural networks (CNNs) utilize tensors to process multi-dimensional data like images and videos.
— Natural Language Processing: Word embeddings and language models are based on tensor representations of text data.
4. Medical Imaging:
— Magnetic Resonance Imaging (MRI): Tensors are employed to process and reconstruct 3D images of the human body.
— Diffusion Tensor Imaging (DTI): Used to study the brain’s white matter pathways.
Code
Tensors are fundamental in libraries like NumPy and TensorFlow when working with multidimensional data. Below are some examples of tensor-related code in Python using NumPy and TensorFlow:
Using NumPy:
Creating Tensors:
import numpy as np# Create a 1D tensor (vector)
vector = np.array([1, 2, 3])
# Create a 2D tensor (matrix)
matrix = np.array([[1, 2, 3], [4, 5, 6]])
# Create a 3D tensor
tensor_3d = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
Tensor Operations:
# Element-wise addition
result = matrix + matrix# Scalar multiplication
result = 2 * matrix
# Matrix multiplication
result = np.dot(matrix, matrix)
Using TensorFlow:
Creating Tensors:
import tensorflow as tf# Create a constant tensor
constant_tensor = tf.constant([1, 2, 3])
# Create a tensor with random values
random_tensor = tf.random.uniform(shape=(2, 3))
# Create a tensor with all zeros
zeros_tensor = tf.zeros(shape=(3, 3))
# Create a tensor with all ones
ones_tensor = tf.ones(shape=(2, 2))
Tensor Operations:
# Element-wise addition
result = tf.add(constant_tensor, constant_tensor)# Scalar multiplication
result = 2 * constant_tensor
# Matrix multiplication
matrix1 = tf.constant([[1, 2], [3, 4]])
matrix2 = tf.constant([[5, 6], [7, 8]])
result = tf.matmul(matrix1, matrix2)
Automatic Differentiation (Gradient Calculation):
x = tf.constant(2.0)
y = x**2
# Calculate the gradient of y with respect to x
grad = tf.gradients(y, x)# Create a session and run the graph
with tf.Session() as sess:
result = sess.run(grad)
print(result) # Output: [4.0]
These examples demonstrate how to create tensors and perform basic operations with them using both NumPy and TensorFlow, two popular libraries for working with tensors in Python. Depending on your specific use case, you may choose one library over the other, with TensorFlow being especially popular for deep learning and machine learning tasks due to its automatic differentiation and GPU support.
Conclusion
Tensors represent a mathematical construct that transcends the boundaries of multiple disciplines, serving as a unifying language for describing complex, multidimensional phenomena. Their formalism allows scientists, engineers, and researchers to model and manipulate data effectively, enabling groundbreaking advancements in fields as diverse as physics, engineering, computer science, and medicine. As technology continues to evolve, tensors will undoubtedly remain an essential tool in the arsenal of scientists and innovators, facilitating the exploration of the intricacies of our universe and the development of cutting-edge solutions to the world’s most pressing challenges.

Be the first to comment