
In the world of supply chain management, ensuring the quality of the products you source is crucial to success. A single defective part can disrupt the entire supply chain and erode customer trust. In this blog, we’ll explore how to use a 1-Proportion Test in Minitab to assess the defect rate of fuel gauges produced by a supplier for an automobile manufacturer.
UNDERSTANDING THE PROBLEM
Imagine a scenario where your company manufactures vehicles and sources fuel gauges from a supplier. While your supplier is reputable, your automobiles represent your high-quality brand and part of your promise to customers is your focus on safety. While you don’t want any defective parts, you understand normal variability and set a 2% defective rate as the acceptable threshold for a supplier. To test your supplier, you perform a calibration test on a sample set of fuel gauges to determine whether the defect rate exceeds the acceptable threshold.
COLLECTING THE DATA
Your team selects 500 fuel gauges supplied during the previous week and conducts calibration tests on them. Out of the 500 fuel gauges, you identify 18 that are calibrated incorrectly.
1-PROPORTION TEST: WHAT IS IT?
A 1-Proportion Test, also known as a one-sample proportion test or a binomial proportion test, is a statistical tool used to determine whether the proportion of a certain characteristic in a sample differs significantly from a known or hypothesized population proportion. In our case, we want to ascertain whether the defect rate (proportion of faulty fuel gauges) is greater than the specified 2%.
SETTING THE HYPOTHESIS
The hypotheses for this test are:
- Null Hypothesis (H0): The defect rate is equal to or less than 2% (p ≤ 0.02)
- Alternative Hypothesis (Ha): The defect rate is greater than 2% (p > 0.02)
PERFORMING THE TEST IN MINITAB
-
Choose Stat > Basic Statistics > 1 Proportion.
-
Choose Summarized data.
-
In Number of events, type 18.
-
In Number of trials, type 500.
-
Check Perform hypothesis test.
-
In Hypothesized proportion, type 0.02.
-
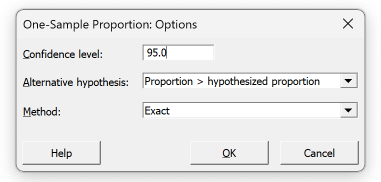
Click Options.
-
Complete the dialog box as shown below, then click OK.
INTERPRETING THE RESULTS
The results suggest the defect rate is higher than 2%:
- The 95% lower bound for the defect rate is 2.3395%, which is higher than 2%
- The p-value (0.013) is below α (0.05)
Since the p-value is below 0.05, we can reject the null hypothesis and conclude that the defect rate is higher than 2%.

Now that you have discovered that the defect rate is higher than expected, you need to ensure that your measurement system was correct. If there was any unwanted bias or variance in your measurement process, you may have mistakenly identified that the fuel gauges were indeed faulty. (Luckily, Minitab has a Measurement System Analysis module designed specifically for just this purpose!)
However, if you are confident in your measurement system, you might consider requesting that the supplier redesign the fuel gauge to improve accuracy. Or, perhaps it’s time to find a new supplier who can provide the quality parts you need to keep your supply chain running smoothly.
REMEMBER TO CONSIDER THE SAMPLE SIZE
The sample from the manufacturing process must be taken randomly. If all 500 fuel gauges came from the same lot or had the same manufacture date, the analysis would exclude lot-to-lot variation or sources of variability over time. The results might then be biased, especially if the sample consisted of an exceptionally good or bad set of parts.
FUELING SMARTER DECISIONS WITH MINITAB
By using a 1-Proportion Test in Minitab, supply chain managers can make data-driven decisions about the quality of sourced products. This type of analysis empowers businesses to take appropriate actions, such as working closely with suppliers to improve manufacturing processes, ensuring smoother supply chains and higher customer satisfaction.
Ready to put your suppliers to the test and improve quality?


Be the first to comment