Overfitting occurs when a model captures data relationships that are too specific, signifying that the model is too complex, thus predictions are not accurate for non-model related data. This is not a new topic or concept, however I recently reviewed some basic optimizer methods and the explanations are clearer. I thought it might be nice to briefly summarize the different optimizers.
A neural network is composed of layers, where each layer has nodes. The node values of each layer are calculated from left to right, such that the estimated output (y_hat) is compared with a known (y), using a cost function J(w,b). This comparison allows us to estimate two key parameters, weights (w) and bias (b), that capture the ‘spaces between the feature space data points’ in terms of slope and intercept respectively.
By changing the way we calculate the weights and bias we can make the estimate values ideal for making J(w,b) as small as possible in the shortest amount of time, thus giving us the correct estimate of y_hat (meaning that y_hat equals y, thus allowing us to predict the output of given data). Some ways to make the weights and bias values ideal, ideal meaning iteratively estimated in a way that y_hat quickly equals to y, consists of using the following methods that:
- optimize the change in parameters based on the backpropagation gradients (dJ/dw, dJ/db) AND the current parameter values (w, b) for layers (L1 regularization, L2 regularization)
- optimize the change in parameters based on the backpropagation gradients (dJ/dw, dJ/db) (Momentum, RMSprop, Adam)
Methods 1 tries to control the MAGNITUDE of the backpropagation gradients by adding a scaling quantity to the gradients. The scaling quantity is composed of an average of feature values and a constant (lambda *(1/m)), where lamba is a hyperparamter and m is the number of examples (or rows) in the input. We can adjust lambda (make it small (0.001) or large (0.1)) to make the gradients most suitable (CLOSE TO THE ORIGINAL GRADIENT VALUES or LARGE) at each iteration, for ideally estimating w and b such that y_hat will quickly equal y.
Method 2 tries to control the ESTIMATE of the backpropagation gradients by modifying the gradients using an Exponential Weighted Average (EWA). The exponential weighted average equation allow initial estimates to not be influenced by noise or erratic changes, thus outputting a value that changes smoothly per iteration while capturing changes.
There are three types of moving average formulations: Simple Moving Average (SMA), Weighted Moving Average (WMA), and Exponential Moving Average (EMA) also known as Exponentially Weighted Moving Average (EWMA) or EWA. The EWA includes the attributes of the SMA and WMA.
SMA
As a quick review, in statistics, the SMA is calculated by adding up all the data points during a specific period and dividing by the window/period length. SMA is the most simplistic and reliable way to estimate an observation variable over a period of data, but it does not: 0) consider recent observations as more important than past observations, nor 1) consider past observations before the window/period into the estimate.
y_hat_{k} = \sum_{window_start=0}^{window_end=i+k}y_{i} / k
where k is the window length (k) and y are the data observations.
WMA
The WMA improves upon the SMA, by considering recent observations as more important than past observations by applying a larger weight to data points at the end of the window, than data points at the beginning of the window.
y_hat_{k} = \sum_{window_start=0}^{window_end=i+k}w_{i}*y_{i} / \sum_{window_start=0}^{window_end=i+k}w_{i}
where w is an array the same length as the window to weight specific data points of y.
EWA
The WMA can be rewritten where the weight and y are written in terms of an exponential series.
y_hat_{k} = y_{k} + [(1-beta)y_{k-1} + (1-beta)² y_{k-2} + … + (1-beta)^k y_{0}] / [1 + (1-beta) + (1-beta)² + … + (1-beta)^k]
where beta is a constant value from 0 to 1 that depends on the length of data. The advantage of EWA is to make recent data points more important than previous data points, while considering past values of y.
Demonstrate SMA, WMA, and EWA
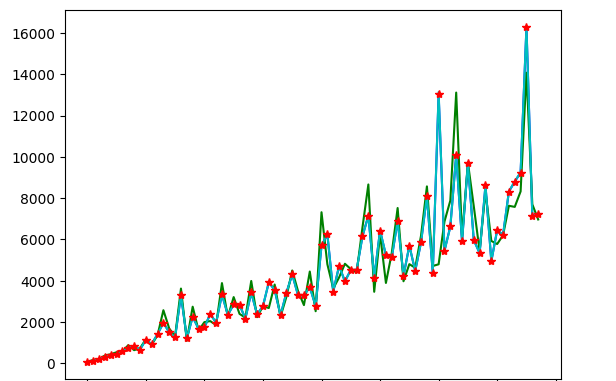
Using a Google Public dataset, the three functions can be visualized with real data.
!gsutil cp gs://cloud-training/mlongcp/v3.0_MLonGC/toy_data/taxi*.csv /kaggle/working
import numpy as np
import pandas as pddf = pd.read_csv('taxi-test_toy.csv')
# I add an increasing trend in the data so that we can see the performance
# of the algorithms more clearly
y = [val*ind for ind, val in enumerate(df['fare_amount'])]
x = np.arange(len(y))
k = 10 # window size of moving average
def moving_avgs(x, y, k):
sma_y_hat = []
wma_y_hat = []
ema_y_hat = []
y_downsample = []
# Recommended value for beta :
# https://www.vskills.in/certification/tutorial/the-exponential-moving-average-ema-model-2/
beta = 2/(len(x)+1)
print('beta: ', beta)
x_downsample = np.arange(0, len(y)-k, k)
for i in range(0, len(y)-k, k):
# SMA
sma_y_hat.append(sum(y[i:i+k])/k)
# WMA
# make a weight vector, where the last values are larger than the initial values
weight = np.arange(k)
wma_y_hat.append(sum( y[i:i+k] * weight ) / sum(weight) )
# EMA
num_series = [y[j]*(1-beta)**j for j in range(i,i+k)]
denom_series = [(1-beta)**j for j in range(i,i+k)]
ema_y_hat.append(sum(num_series) / sum(denom_series))
y_downsample.append(np.mean(y[i:i+k]))
return sma_y_hat, wma_y_hat, ema_y_hat, x_downsample, y_downsample
sma_y_hat, wma_y_hat, ema_y_hat, x_downsample, y_downsample = moving_avgs(x, y, k)
def rmse(y_true, y_pred): # Root mean square error
y_true = np.array(y_true)
y_pred = np.array(y_pred)
return np.sqrt(np.mean(np.square(y_pred - y_true)))sma_rmse = rmse(sma_y_hat, y_downsample)
wma_rmse = rmse(wma_y_hat, y_downsample)
ema_rmse = rmse(ema_y_hat, y_downsample)
print('sma_rmse: ', sma_rmse)
print('wma_rmse: ', wma_rmse)
print('ema_rmse: ', ema_rmse)
import matplotlib.pyplot as plt
plt.plot(x_downsample, sma_y_hat, 'b-')
plt.plot(x_downsample, wma_y_hat, 'g-')
plt.plot(x_downsample, ema_y_hat, 'c-')
plt.plot(x_downsample, y_downsample, 'r*')
Now that we know how these algorithms work and perform with data, lets apply them to the gradients (meaning exchange y for dw or db) to realize the Momentum and RMSprop formulations. The EWA equation can be written per iteration, instead of the exponential series formula above.
y_hat_{0} = x_{0}
to
y_hat_{k} = beta*x_{k} + (1-beta)*y_{k-1}
Replace y with dw, and substitute x_{k} with the previous value of y_hat, we can obtain:
y_hat_{k} = beta*y_hat_{k-1} + (1-beta)*dw
In many papers, y_hat is called v_dw the exponential average.
v_dw_{k} = beta*v_dw_{k-1} + (1-beta)*dw
Momentum uses the exponential average of the one-norm and two-norm components of the change in w and b. And, RMSprop uses the exponential average of the squared one-norm and two-norm components of the change in w and b. The famous Adam and AdamW formulations uses a combination of the exponential average and squared exponential average.
# Creates a dataset
N_POINTS = 10# X is a list
X = tf.constant(range(N_POINTS), dtype=tf.float32)
print('X: ', X)
Y = 2 * X + 10
print('Y: ', Y)
Below are subfunctions to iterate gradient descent for the different optimization algorithms.
def create_dataset(X, Y, epochs, batch_size):
dataset = tf.data.Dataset.from_tensor_slices((X,Y))# epochs is the number of times that it repeats the data in X and Y
# batch cuts the data into chucks of batch_size, where the number of batch chucks is a 3rd dimension
dataset = dataset.repeat(epochs).batch(batch_size, drop_remainder=True)
return dataset
def loss_mse(X, Y, w0, w1):
# Y_hat = w0 * X + w1
Y_hat = tf.math.multiply(w0, X) + w1
errors = (Y_hat - Y)**2
return tf.reduce_mean(errors)
def compute_gradients(X, Y, w0, w1):
with tf.GradientTape() as tape:
loss = loss_mse(X, Y, w0, w1) # loss at every [example datapoint]
# dJ/dw
dJ_dw = tape.gradient(loss, [w0, w1])
return dJ_dw
The iterative run is in a function because I wanted to see the effects of re-initializing w0 and w1 from past iterations and switching optimizers from one iterative run to the next.
I was imagining that perhaps, like adaptive learning rate, a different optimizer could be used at a strategic training point to improve results. Unfortunately, there was not much of a difference in convergence time when using various optimization techniques interchangeably.
def initialize_vals():
# Random initialization with uniform distribution
rand_float = np.random.default_rng().uniform(0,1,size=(1,1))[0][0] * 0.01
w0 = tf.Variable(int(rand_float*100)/100)
rand_float = np.random.default_rng().uniform(0,1,size=(1,1))[0][0] * 0.01
w1 = tf.Variable(int(rand_float*100)/100)rand_float = np.random.randn(1,1)[0][0] * 0.01
v_dw0 = tf.Variable(int(rand_float*100)/100)
rand_float = np.random.randn(1,1)[0][0] * 0.01
v_dw1 = tf.Variable(int(rand_float*100)/100)
rand_float = np.random.randn(1,1)[0][0] * 0.01
s_dw0 = tf.Variable(int(rand_float*100)/100)
rand_float = np.random.randn(1,1)[0][0] * 0.01
s_dw1 = tf.Variable(int(rand_float*100)/100)
return w0, w1, v_dw0, v_dw1, s_dw0, s_dw1
def iterative_run(dataset, which_way, m, L, beta1, beta2, epsilon, w0, w1, v_dw0, v_dw1, s_dw0, s_dw1):
out = []
# This is giving a batch of data per step, therefore for each loop/step
# it has BATCH_SIZE number of data points making m=BATCH_SIZE
for step, (X_batch, Y_batch) in enumerate(dataset):
# Backpropagation computes the sum of partial derivatives across all examples in a BATCH
dw0, dw1 = compute_gradients(X_batch, Y_batch, w0, w1)
# print('dw0 : ', dw0)
# print('dw1 : ', dw1)
# ----------------------------------------
if which_way == 'basic':
# w0 = w0 - LEARNING_RATE*dw0
# w1 = w1 - LEARNING_RATE*dw1
w0.assign_sub(dw0 * LEARNING_RATE)
w1.assign_sub(dw1 * LEARNING_RATE)
# These methods optimize the change in parameters based on the gradients AND
# the current parameter values for layers
elif which_way == 'L1_regularization':
# L1 regularization
# So to add regularization, I need the sum w across the layers
w0_sum = w0 # there is just one layer
w1_sum = w1 # there is just one layer
dw0_r = dw0 + (L/BATCH_SIZE * w0_sum)
dw1_r = dw1 + (L/BATCH_SIZE * w1_sum)
w0.assign_sub(dw0_r * LEARNING_RATE)
w1.assign_sub(dw1_r * LEARNING_RATE)
elif which_way == 'L2_regularization':
# L2 regularization
# So to add regularization, I need the sum w across the layers
w0_sum = w0 # there is just one layer
w1_sum = w1 # there is just one layer
dw0_r = dw0 + (L/BATCH_SIZE * np.square(w0_sum))
dw1_r = dw1 + (L/BATCH_SIZE * np.square(w1_sum))
w0.assign_sub(dw0_r * LEARNING_RATE)
w1.assign_sub(dw1_r * LEARNING_RATE)
# These methods optimize the change in parameters based on the gradients
elif which_way == 'momentum':
# Momentum
v_dw0 = beta1*v_dw0 + (1-beta1)*dw0
v_dw1 = beta1*v_dw1 + (1-beta1)*dw1
w0.assign_sub(LEARNING_RATE * v_dw0)
w1.assign_sub(LEARNING_RATE * v_dw1)
elif which_way == 'rmsprop':
# Rmsprop
s_dw0 = beta2*s_dw0 + (1-beta2)*np.square(dw0)
s_dw1 = beta2*s_dw1 + (1-beta2)*np.square(dw1)
w0.assign_sub(LEARNING_RATE * dw0/(np.sqrt(s_dw0) + epsilon))
w1.assign_sub(LEARNING_RATE * dw1/(np.sqrt(s_dw1) + epsilon))
if step % 100 == 0:
loss = loss_mse(X_batch, Y_batch, w0, w1) # loss per epoch
print(MSG.format(step=step, loss=loss, w0=w0.numpy(), w1=w1.numpy()))
out.append(loss)
loss_final = loss
import matplotlib.pyplot as plt
plt.title(f'{which_way}')
plt.plot(out)
return loss_final
Below is the main function that runs the subfunctions. The main function stops when a certain convergence accuracy is reached.
# Training loop
EPOCHS = 100
BATCH_SIZE = 2
LEARNING_RATE = 0.02MSG = "STEP {step} - loss: {loss}, w0: {w0}, w1: {w1}\n"
dataset = create_dataset(X, Y, epochs=EPOCHS, batch_size=BATCH_SIZE)
print('dataset : ', dataset)
m = BATCH_SIZE
beta1 = 0.9
beta2 = 1 - 2/(len(dataset)+1) # 0.999 0.9960079840319361
# methods = ['basic']
# methods = ['L1_regularization'] # did not converge with learning_rate - close
# methods = ['L2_regularization'] # did not converge with learning_rate - close
methods = ['momentum']
# methods = ['rmsprop'] # did not converge with learning_rate
w0, w1, v_dw0, v_dw1, s_dw0, s_dw1 = initialize_vals()
tot = []
allbool = [False, False, False]
i = 0
while all(allbool) == False:
i = i + 1
print('i: ', i)
for j in methods:
loss_final = iterative_run(dataset, j, m, L, beta1, beta2, epsilon, w0, w1, v_dw0, v_dw1, s_dw0, s_dw1)
tot.append(loss_final)
allbool = [loss_final < 0.0001, abs(w0 - 2) < 0.001, abs(w1 - 10) < 0.001]
assert loss_final < 0.0001
assert abs(w0 - 2) < 0.001
assert abs(w1 - 10) < 0.001
Basic gradient descent and momentum were the fastest to converge using a large learning rate, where as the other optimization methods require a smaller learning rate thus they oscillated around the converging values of w0=2 and w1=10.
- The data and iteration example was motivated by the Google training class : https://github.com/GoogleCloudPlatform/training-data-analyst/blob/master/courses/machine_learning/deepdive2/introduction_to_tensorflow/labs/2_dataset_api.ipynb
Happy Practicing! 👋

Be the first to comment